MTK(W)-PROGRAM LINIER-PERT 6

 

PROGRAM LINIER

1. PENYELESAIAN SISTEM PERTIDAKSAMAAN LINIER DUA VARIABEL

Dalam praktiknya penyelesaian pertidaksamaan linear bisa berwujud daerah diarsir atau sebaliknya daerah penyelesaian pertidaksamaan linear dua variabel yang berupa daerah bersih.

Untuk menentukkan daerah penyelesaiannya, kita bisa melakukan langkah-langkah seperti di bawah ini:

1. Ubahlah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga kita akan memperoleh persamaan linear dua variabel
2. Gambar dari grafikatau garis dari persamaan linear dua variabel tadi.
   Hal ini bisa kita lakukan dengan cara menentukan titik potong sumbu x dan sumbu y dari persamaan.
   Ataupun dapat memakai dua titik sembarang yang dilewati oleh garis. Garis akan membagi dua bidang kartesius
3. Lakukan uji titik yang tidak dilewati oleh garis (substitusi nilai x dan y titik ke pertidaksamaan). Apabila menghasilkan pernyataan yang benar, artinya daerah tersebut adalah penyelesaiannya.
   Tetapi, jika menghasilkan pernyataan salah maka bagian lainnya lah yang merupakan penyelesaiaanya.

Pertidaksamaan linear merupakan pertidaksamaan yang mana peubah bebasnya berbentuk linear (pangkat satu). Kalian tentunya masih ingatkan beberapa kalimat matematika di bawah ini.

• 2x ≥ 4; pertidaksamaan linear satu peubah
• 3x + y < 0; pertidaksamaan linear dua peubah
• x – 2y ≤ 3; pertidaksamaan linear dua peubah
• x + y – 2z > 0; pertidaksamaan linear tiga peubah

Dan kali ini, kami akan membahas seputar pertidaksamaan linear dengan dua peubah.

Gabungan dari dua atau lebih pertidaksamaan linear dua peubah disebut sebagai sistem pertidaksamaan linear dua peubah.

i

Berikut adalah contoh dari sistem pertidaksamaan linear dua peubah:

3x + 8y ≥ 24,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.

ingta...!

(Garis putus-putus digunakan menunjukkan tanda ketidaksamaan < atau >

(Garis bersambung digunakan menunjukkan tanda ketidaksamaan ≤ atau ≥

Untuk lebih memahami daerah himpunan dari penyelesaian pertidaksamaan linear dua peubah. Berikut akan kami berikan contohnya:

Contoh:

Tentukan himpunan penyelesaian dari pertidaksamaan linear di bawah ini:
a. 2x + 3y ≥ 12             c. 4x – 3y < 12
b. 2x – 5y > 20            d. 5x + 3y ≤ 15

Jawab:

a. Langkah pertama adala lukis garis 2x + 3y = 12 dengan cara menghubungkan titik potong garis dengan sumbu X dan sumbu Y.

Titik potong garis dengan sumbu X memilki arti sebagai y = 0, dan didapatkan x = 6 (titik (6,0)).

Titik potong garis dengan sumbu Y artinya x = 0, didapat y = 4 (titik (0,4)).

Garis 2x + 3y = 12 tersebut kemudian akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian, maka dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh disini kita ambil titik (0,0). Lalu disubstitusikan ke pertidaksamaan sehingga akan kita peroleh:

2 x0 + 3x 0 < 12
0 < 12

Sehingga, 0 ≥ 12 salah, yang berarti tidak dipenuhi sebagai daerah penyelesaian.

Jadi, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

b. Langkah pertama adalah menggambar garis 2x – 5y = 20 dengan cara menghubungkan titik potong garis di sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X,  y = 0, didapat x = 10 (titik (10,0))
• Titik potong garis dengan sumbu Y, x = 0, didapat y = –4 (titik (0,–4))

Garis 2x – 5y = 20 tersebut akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil titik uji pada salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

2 x0 – 5 x0 > 20
0 > 20 (salah), artinya tidak dipenuhi.

Sehingga, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

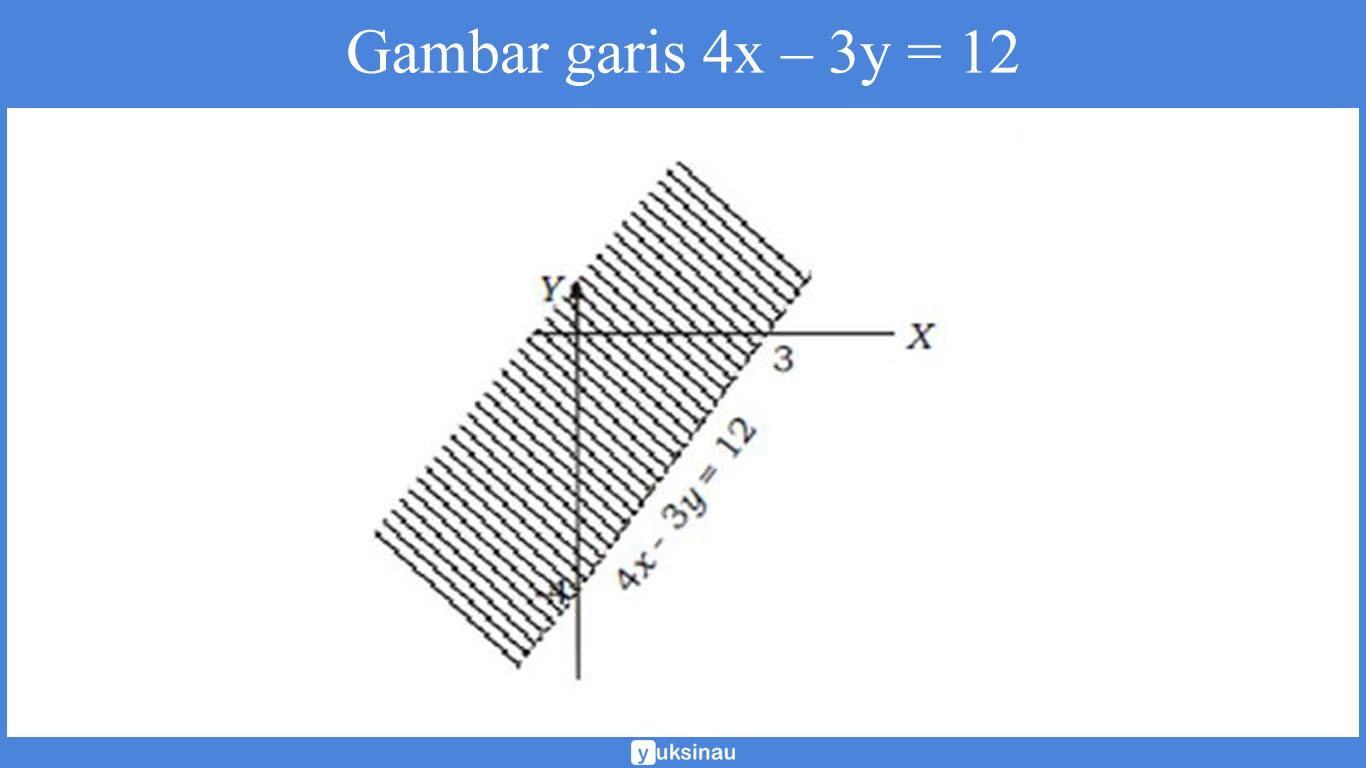
c. Langkah pertama adalah menggambar garis 4x – 3y = 12 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X maka y = 0 didapat x = 3 (titik (3,0))
• Titik potong garis dengan sumbu Y maka x = 0 didapat y = –4 (titik (0,–4))

Garis 4x – 3y = 12 tersebut akan membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

4 x0 – 3x 0 < 12
0 < 12 (benar), yang berarti dipenuhi sebagai daerah penyelesaian.

Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

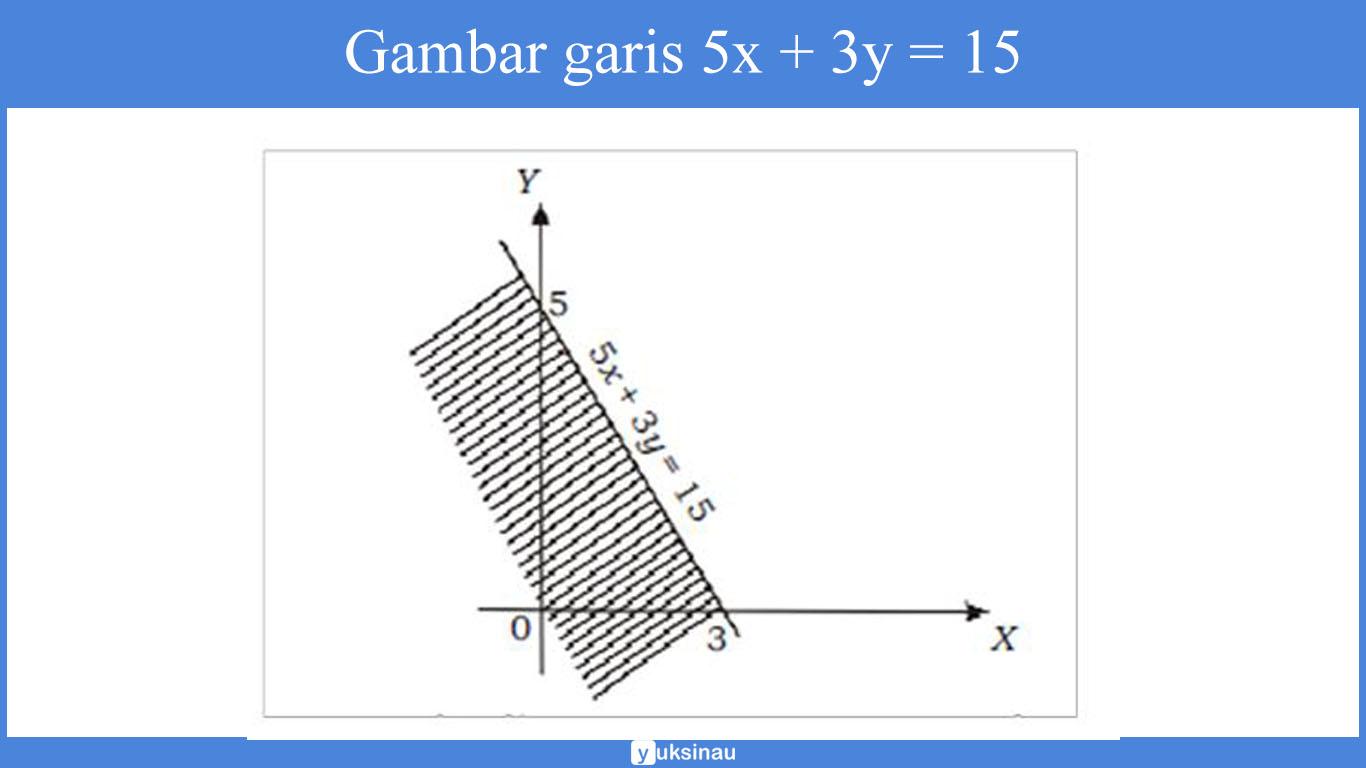
d. Langkah pertama adalah menggambar garis 5x + 3y = 15 dengan cara menghubungkan titik potong garis pada sumbu X dan sumbu Y.

• Titik potong garis dengan sumbu X maka y = 0, didapat x = 3 (titik (3,0))
• Titik potong garis dengan sumbu Y maka x = 0, didapat y = 5 (titik (0,5))

Garis 5x + 3y = 15 tersebut membagi bidang kartesius menjadi dua bagian.

Untuk menentukan daerah yang mana adalah himpunan penyelesaian. Maka kita akan melakukannya dengan cara mengambil salah satu titik uji dari salah satu sisi daerah.

Sebagai contoh kita ambil titik (0,0). Lalu kita substitusikan ke pertidaksamaan sehingga akan kita peroleh:

5 x0 + 3x 0 ≤15
0 ≤ 15 (benar), artinya dipenuhi.

Sehingga, daerah penyelesaiannya yaitu daerah yang terdapat atau memuat titik (0,0). Yakni daerah yang diarsir pada gambar di bawah ini:

Untuk lebih jelasnya lihat vidio berikut

nah sekarang kerjakan soal berikut klik di JANAH

Share this post